ClemensLange/QCDAnalysis -

Contents

ToDo
Completed ToDo/Discussion
Event Selection
Missing ET vs. Electron Isolation Method
Antielectron Method
1. Cross-Section Calculation

ToDo

Implementation

Implementation in SFrame

is it actually correct to take into weighted MC events instead of data points?
implement top baseline selection and test.
Oliver: dump events and look at topology. He doesn't think those events are actually electron fakes but just electrons in jets. Maybe one could remove those in an easier way.

Implementation in Root

Draw two and ratio MET QCD RefFinal 2 jets scaled to unity
Draw random events from distributions (tree variables now available) and fit 100 times
get effiencies for all channels
Do fit for all jet multiplicity bins
do Appendix C fix (Anti-electron contamination)
get other electro-weak stuff in
change jet pT threshold? (is implemented, but probably needs some change). Could e.g. require 3 high pt jets plus another low pt jet.

Admiration

check if track particle Z veto is good (used to be so in CDF)
check if m_W cut biases MET
try if MET is correlated with (anti-)electron eta: plot MET for central (before crack) and fwd (beyond crack) electrons and MET vs. electron eta

Completed ToDo/Discussion

Do TFractionFitter tests: Create Landau with small Gaussian distribution on top and try to fit, repeat for weighted events
- didn't see problems, see attached test script (TestFractionFitter.C and TestFractionFitter.h)

Event Selection

require electron trigger (EF_e20_loose). Was before EF_e15, but this is not filled (not on the menu any more).
reject event if combined muon with pt>20GeV and etcone20<6000GeV
exactly one good electron (pt>20, no crack, eta<2.5, medium)
remove jets that are within dR < 0.4 of electron
skip event, if another jet is within dR<0.52
Zee rejection: skip event, if:
- jet (pt>15,eta<2.5) with nTracks < 3 or
- electron object (pt>15,eta<2.5) with ethad1/(pt-ethad1)<0.12, etcone20<0.15*pt and opposite charge found or
- trackparticle (pt>10,eta<2.5) with NSCT+NPixelHits>=7, |d0|<2mm, |z0*sin(theta)|<10mm and opposite charge found.

Missing ET vs. Electron Isolation Method

Antielectron Method

Currently an antielectron is an electron object that passes the ElectronLoose cuts but not the ElectronMedium cuts.

m_W transverse mass > 20

Cross-Section Calculation

Formulae:

$\begin{equation} %\begin{align} N_n (\mathrm{data}) = K_{W_n} \cdot \left[ N_n(W \rightarrow e^+ e^-) + A_Z N_n (Z \rightarrow e^+ e^-) + A_\tau N_n (W \rightarrow \tau \nu) \right] + K_{Q_n} \cdot \left[ N_n (\mathrm{QCD}) + A_\mathrm{top} N_n (\mathrm{top}) \right] %\end{align} \end{equation}$

X_n(Y): Contribution of process Y to region X:

$\begin{equation} X_n (t\bar{t}) = X_n^\mathrm{sel} (t\bar{t}\mathrm{\:MC}) \cdot \frac{L_\mathrm{data}}{L_{ t\bar{t} \mathrm{\:MC} } } \end{equation} \begin{equation} X_n(Z \rightarrow e^+ e^-) = \frac{ X_n^\mathrm{sel} (Z \rightarrow e^+ e^- \mathrm{\:MC}) }{ D_n^\mathrm{sel} (W \rightarrow e \nu \mathrm{\:MC}) } \cdot \frac{ G (W \rightarrow e \nu \mathrm{\:MC}) } { G (Z \rightarrow e^+ e^- \mathrm{\:MC}) } \cdot \frac{ 1 }{ R_{WZ} } \cdot N_n (W \rightarrow e \nu) \end{equation} \begin{equation} X_n(W \rightarrow \tau \nu) = \frac{ X_n^\mathrm{sel} (W \rightarrow \tau \nu \mathrm{\:MC}) }{ D_n^\mathrm{sel} (W \rightarrow e \nu \mathrm{\:MC}) } \cdot \frac{ G (W \rightarrow e \nu \mathrm{\:MC}) } { G (Z \rightarrow \tau \nu \mathrm{\:MC}) } \cdot \frac{ 1 }{ R_{WZ} } \cdot N_n (W \rightarrow e \nu) \end{equation} \begin{equation} X_n(W \rightarrow e \nu) = \frac{ X_n^\mathrm{sel} (W \rightarrow e \nu \mathrm{\:MC}) }{ D_n^\mathrm{sel} (W \rightarrow e \nu \mathrm{\:MC}) } \cdot N_n (W \rightarrow e \nu) \end{equation}$

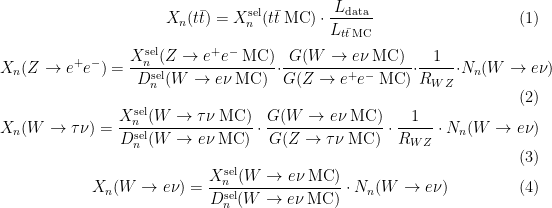
Factorising all electroweak contributions one can write:

$\begin{equation} X_n (\mathrm{ewk}) = x_n \cdot N_n (W \rightarrow e \nu) \end{equation}$

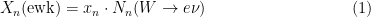
with $x_n$ defined from equations above.

ATLAS: ClemensLange/QCDAnalysis (last edited 2010-02-23 22:35:24 by ClemensLange)